
 [罗戈导读]模型成立的一个重要前提条件是平均的需求,这是考虑到人体每天消耗的食物量是比较均衡的,而且没有暴饮暴食。
[罗戈导读]模型成立的一个重要前提条件是平均的需求,这是考虑到人体每天消耗的食物量是比较均衡的,而且没有暴饮暴食。

模型成立的一个重要前提条件是平均的需求,这是考虑到人体每天消耗的食物量是比较均衡的,而且没有暴饮暴食。
在更多的现实场景中,需求是随机的,是持续变动的,很少会有一成不变的情况。
由于需求具有随机性,企业更多地使用固定订货周期,它的特点和买菜模型有些类似,订货间隔的时间是固定的,物料计划员定期检查需求和库存情况,根据前置时间下订单。
固定订货周期模型的最大库存持有量不仅包含了需求的平均值,还有安全库存,用于抵消随机需求造成的缺货,这是这篇文章重点想要探讨的话题。
在介绍公式之前,先简单谈一下随机的概念。说起随机,我首先想到了一个英语单词Random。在Excel中有一个函数公式“RAND()”,输入后会得到一个介于0到1之间的数,每次出来的结果都不重复,它很好地解释了随机这个词的本意。
在概率统计学里,随机性是指事件可能出现的结果是已知的,只是不知道下一次会出现哪种结果,比如上面的公式结果只会在0到1之间,但我们不知道会出现什么数值。范围已知,结果未知,这才是随机。
近年来供应链有个热门词语,叫做不确定性,它有个别名叫“黑天鹅事件”。举个例子,2021年3月23日,一艘中国台湾长荣集团货轮“Ever given”号,在经过苏伊士运河时发生事故,横向卡在运河中,堵塞了双向交通。
此类事件是无法预知的意外,特点就是不确定,我们完全不知道事件可能会出现哪些结果。这样看来,随机性和不确定性是两回事儿,在库存订货模型中,我们谈论的是随机性的问题,这样才可以使用到正态分布进行分析,而不确定性事件是不能预见的,就不在订货模型中讨论了。
再举个例子,2022年俄罗斯和乌克兰发生冲突,导致了欧洲能源供应紧张,价格大涨。面对昂贵的取暖费账单,欧洲老百姓被迫选择平价替代品,大量采购了中国制造的电热毯等取暖设备,这些产品的订单从当年7月份开始爆增,这种超出预期的需求在俄乌冲突发生前是想象不到的,订货模型是没法应对这种场景的,所以“黑天鹅事件”不在本文的讨论范围之内。
1.最大库存量公式
固定订货周期模型先要设定一个最大库存持有量,简称最大库存量,也叫做Base Stock。订货的周期是固定的,可以是每月、每周,或是每天。订货数量是使用最大库存量减去现有库存和已预定的库存。
每次订货的数量是变动的,因为订货后数量要达到最大库存量,而现有库存数量是随着需求的波动而上下变动的,它不是稳定地消耗的,所以订货量是可变的。
来看最大库存量的计算公式。
最大库存量=(需求均值×(二次订货间隔时间+前置时间))+(K×(需求标准差×√((二次订货间隔时间+前置时间)))
公式中有三个概念,分别是需求均值、K值和需求标准差,要把它们讲清楚,首先要来了解另一个概念,那就是著名的正态分布。
2.正态分布、均值和标准差
在自然界中有一种神奇的现象,处于平均水平的情况比较多,高出或低于平均的情况比较少,这种现象很常见。由于这种分布情况很普通,所以它被叫做Normal Distribution,Normal就是正常、平常的意思。
相比之下,其他类型的分布就显得有些特殊,适用范围也小很多。只有正态分布才具有普遍适用性,值得我们重点研究。
举个例子,人类的身高就符合正态分布,如果平均身高是175厘米,则大多数人的身高在165至185厘米之间,统计身高和对应的概率值,大体上是这样的,横轴是身高,竖轴是出现的概率。
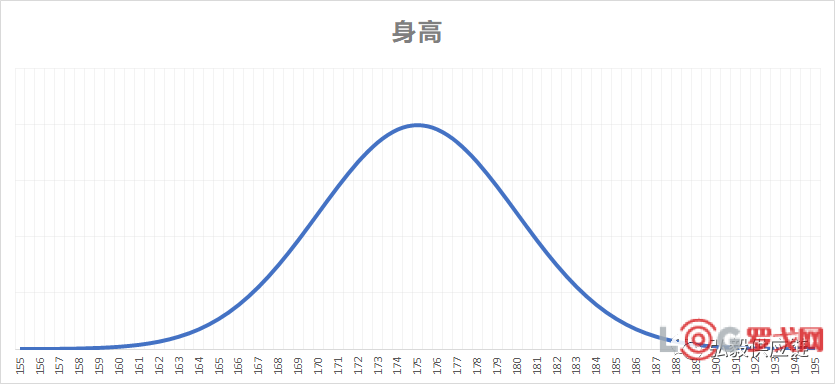
这条曲线左右对称,像是一座小山,中间高,两边越来越低。这座山坡的最高点就是均值或平均值,它决定了山坡的高度。均值的计算公式很简单,把所有数相加,再除以数据的个数就可以了,在Excel里的公式是“Average(数据1,数据2,…,数据N)”。
每个数值和均值之间都有差,比如身高180厘米和均值175的差距是5厘米。如果我们把所有的值和均值的差的平方相加,然后除以数据个数,就可以得到方差(Variance),再把方差开平方根,就得到了标准差(Standard Deviation),就是所谓的“西格玛”,符号是σ。
标准差代表什么意思?它用来描述随机变量的波动情况,标准差越大,说明数据和均值的差距很大,意味着波动很厉害。反映在身高上,有些人可能很高,还有些人很矮,相差得很远。标准差越小,说明大家的身高都差不多,比较接近于平均值。
标准差的计算过程显然要比均值麻烦许多,先要算出每个结果和均值的差,然后求平方的均值,再开根号,计算量很大。好在Excel里有相关的函数,我们只需要把数据准备好,然后输入“STDEV.S(数据1,数据2,…,数据N)”就可以了。
说了那么多均值和标准差的内容,这与订货模型有什么关系?回到上面的公式,它可以分为两个部分,前面一半是计算循环库存(Cycle Stock),后一半是关于安全库存(Safety Stock)。
3.循环库存
循环库存是指“收到客户订单时逐渐消耗,在收到供应订单时循环补充”的库存。它的主要特点是循环补充,这是与安全库存最大的区别之处。在整个订货周期过程中,当我们下了订单后,需要经过一段时间后才能收到货物,这段时期叫做前置时间(Lead Time)。
固定订货周期意味着每隔一段时间才会下单,例如采购员每个星期订货一次。每次下的订单至少要能覆盖二次订货间隔和前置时间,这样才能保证这段时间的需求都被照顾到了。
假设A商品的订货间隔是7天,也就是每隔7天需要订货一次,订货日分别是7月4日、11日和18日。到货的前置时间是2天,当4日订货后,6日货物送到,11日的订单,在13日到货。
7月4日的这张订单,不仅要满足至11日的需求,还要继续延伸两天至13日,因为11日的订单要在那天才到达。A商品的需求要覆盖前置时间加上订货间隔的全部,这样才保障在循环周期里的供应,所以这部分的库存被叫做循环库存。
它的计算公式是使用需求的均值乘以二次订货间隔与前置时间的总和。
循环库存=需求均值×(二次订货间隔时间+前置时间)
需求具有随机性,有时多,有时少,在正态分布之下,我们知道它的范围,但不知道下一次会需要多少量,所以需要有安全库存作为缓冲。在7月12日那天,如果没有安全库存在下面垫着,恐怕就缺货了,预计库存已经非常接近于0,11日下的订单还没到货,库存水平处于周期中的最低点。
4.安全库存
那么安全库存怎么设定?这就关系到订货模型公式的后半部分,回顾一下公式
安全库存=K×(需求标准差×√((二次订货间隔时间+前置时间)))
K值终于登场了,在有些教材里也叫Z值,都是一回事儿,它代表了一个系数,从公式上看,系数越大,安全库存也就越大,越是不容易缺货。
如何定义这个值呢?有一种通常的做法是领导来决定,对标一下行业里的龙头企业,如果达到了95%的交货率,那我们也定这个指标,在100次订单里,有95次能交货,缺货率只有5%。
目标有了,如何转换成K值呢?我们还是要去正态分布中寻找答案,一个标准差能够覆盖68.26%的数据,也就是均值左右各34.13%,这是标准差的重要意义。
根据概率的基本定律,概率的最大值为1,正态分布又是对称的,所以左右半边各占了50%。一个标准差的累计概率是50%+34.13%,等于84.13%,而两个能覆盖到97.72%的数据。在身高分布案例中,只要身高达到185厘米,就能超越97.72%的人了。
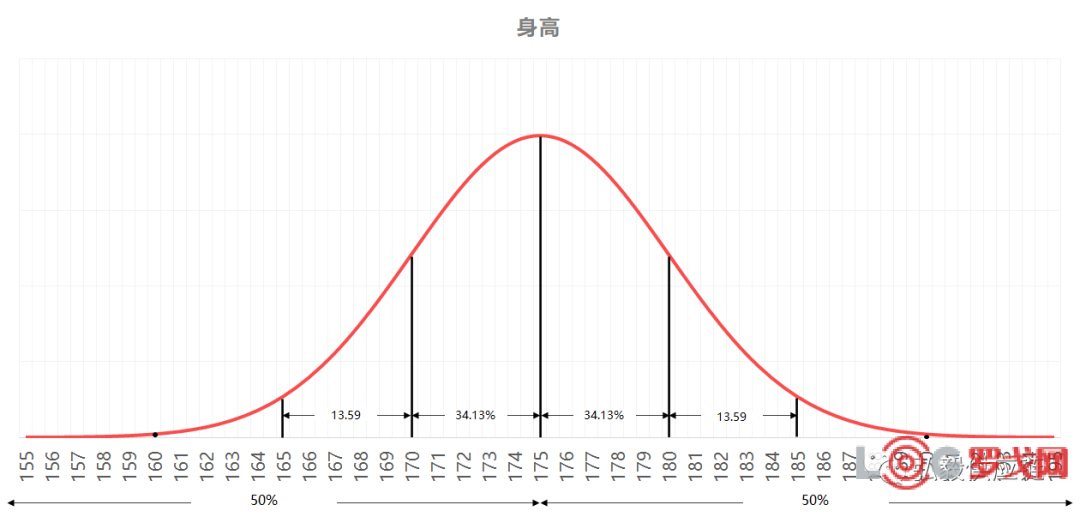
在订货模型中,2个标准差就能够满足97.72%的交货率或服务水平。根据公式,想要实现95%的交货率,对应的K值是1.645,也就是1.645倍的标准差。这段文字可能有些烧脑,如果不理解也没关系,只需要明白K值越大,安全系数就越高。
有一点我们需要了解,K值不是线性关系,标准差从0到1可以增加34.13%的覆盖面,从1到2只有13.59了,越往后就更少了,属于边际效应递减。
5.如何找到K值?
有一种办法可以计算K值,在Excel中输入公式“NORM.S.INV(累积概率)”,就能立即获得对应的K值。
6.数据模拟
我用一组数据来模拟一下订货模型的情况。
假设A商品每天的需求符合正态分布,均值是100,标准差是40。二次订货间隔是7天,前置时间是2天,要求的服务水平是95%。
每次订货数量是用1097减去期初库存,这样就能使得在库数量和订货数量之和始终都是1097。具体数据如下图。
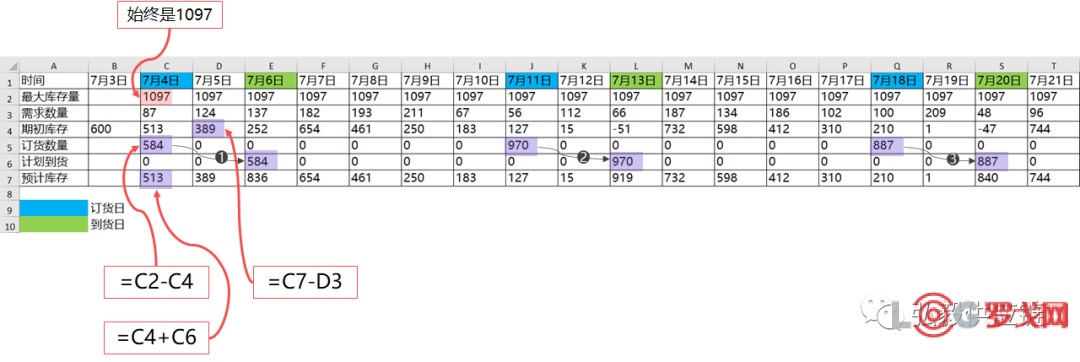
我分别在7月4日、11日和18日订货,到货日期是7月6日、13日和20日。在7月3日的期初库存有600,4日的需求是87,所以4日的期初库存是600减去87,等于513。这一天的订货数量就是1097减去513,等于584。
在7月5日,期初库存用前一日的预计库存513减去需求124,得到了389,这也是当日的预计库存。7月6日的期初库存同样是用前一日的预计库存389减去当日需求137,结果是252,由于当天有到货584,所以预计库存是836。
后续的两次订单分别在13日和20日到货,整个过程中预计库存始终大于零,尽管在7月12日和19日时库存很低,但凭借着安全库存,让服务水平得到了保障。
以上就是经典的固定订货周期模型,此外还有一些模型,比如固定订货数量模型、或是混合订货模型等,它们各有适用的场景。

菜鸟全球供应链再升级:亚太仓配网络覆盖10个国家地区
1400 阅读
九识、新石器、白犀牛、菜鸟、京东物流、美团、顺丰等布局的万亿赛道,谁将成为“领头羊”?
1190 阅读
Gartner供应链25强十年(2016~2025)演进的洞察
1115 阅读Temu正式进军土耳其市场 推出“一日达”配送服务
1022 阅读王卫1110亿元、赖梅松289亿元、杨绍鹏213亿元、喻渭蛟夫妇176亿元......物流领域最新财富榜出炉!
981 阅读守护车轮上的健康!运满满首站货车司机公益体检活动落地宿迁
934 阅读亚马逊当日或次日达服务年内扩展至4000个美国小城镇
900 阅读阿里最新合伙人名单出炉:精简至17人,9人退出,无新增
878 阅读亿通国际针对航运业的碳管理解决方案
835 阅读菜鸟集运6月香港累计注册用户同比激增95%
813 阅读